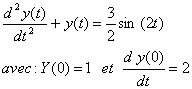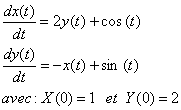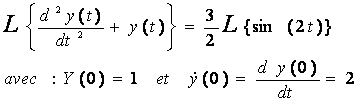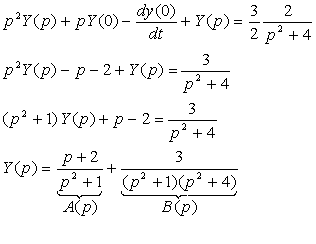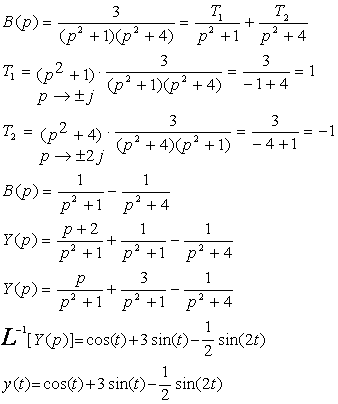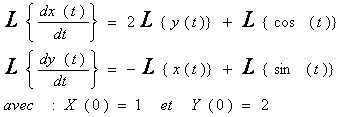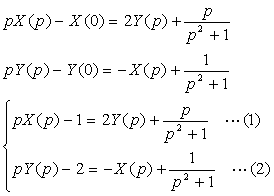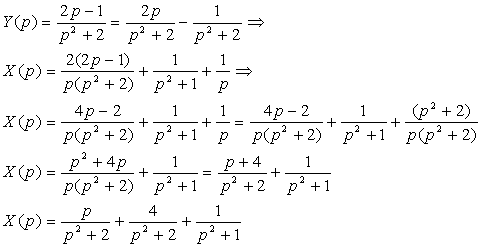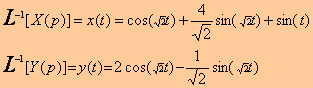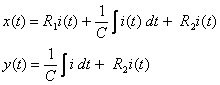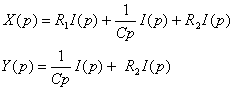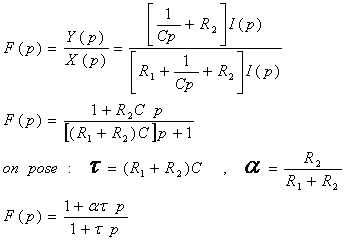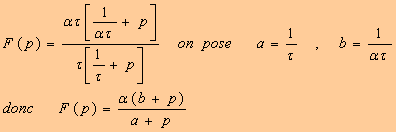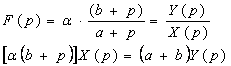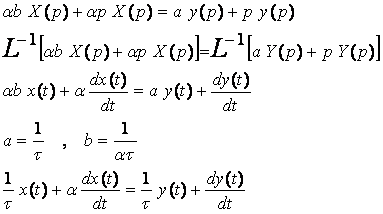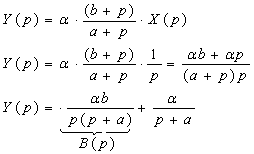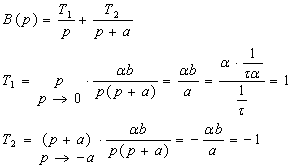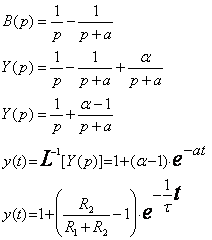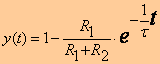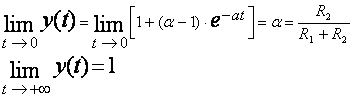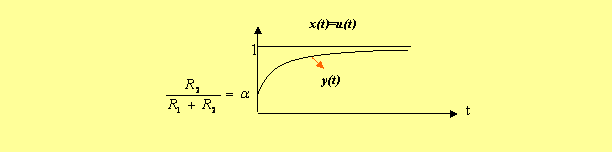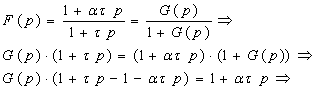|
|
|||||||||||||||
|
Download |
|||||||||||||||
 |
|
Série d’exercices Exercice 01 :
Exercice 02 :
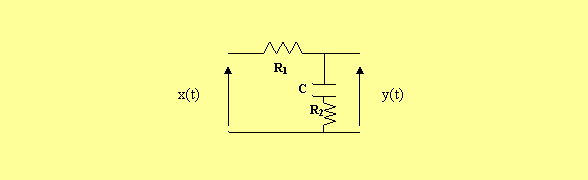
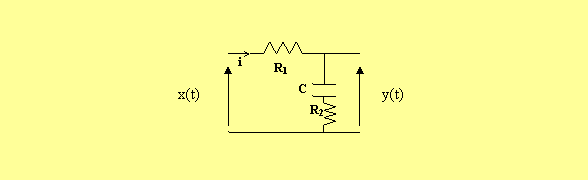
Je tien a préciser qu’il faut impérativement s’exercer a résoudre beaucoup d’exercices, tout au tend comprendre les significations physiques Exercice 03: Soit le circuit électrique d’un correcteur à retard de phase.
1. Calculer la fonction de transfert du circuit électrique. 2. Ecrire l’équation différentielle de ce circuit. 3. Tracer sans effectuer aucun calcul, la réponse de ce circuit à entrée échelon. 4. Décrire ce circuit par un schéma bloc a boucle.
Solution de la série d’exercices Exercice 01 :
On appliquant le théorème de la dérivation, on a :
On décompose en éléments simples :
Exercice 02 :
On appliquant le théorème de la dérivation, on a :
On résolvant le système d’équation on a:
On appliquant la transformée de Laplace inverse sur X(p) et Y(p) obtenus, on obtient:
Exercice 03:
Application de la transformée de Laplace :
1.
On peut l’écrire sous autre forme :
2. Le circuit est un correcteur à retard de phase.
Donc on aboutit a :
Finalement l’équation différentielle est :
3.
La réponse a un échelon unitaire :
La décomposition en éléments simples :
La courbe de la réponse de y(t) si on injecte un signal x(t) a un échelon unitaire :
4.
|
|
[Home] [Introduction] [Sommaire] [Cours] [Exercices] [Série d'exercices+Solution] [Série d'examens+Solution] [Exercices non résolus] |