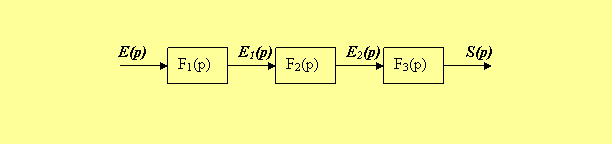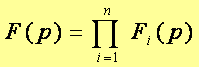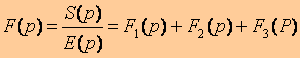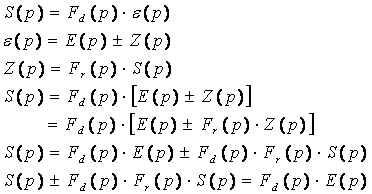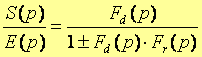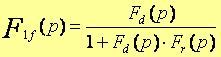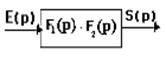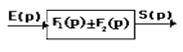Download

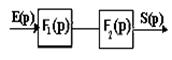
Transformation des schémas fonctionnels 

Par définition, un système asservi est un système bouclé, or lors de conception, on considère fréquemment la chaîne ouvert tout d'abord et chaîne fermée par la suite.

La fonction de transfert des boucles fermées et ouverts sont détermines en considérant les connexions types des éléments qui constitue le système. La transformation des schémas fonctionnels est un moyen pour réduire ce dernier en un schémas plus simple ; souvent cette transformation est nommée forme canonique du schémas fonctionnels.  

Il existe trois modes de connexions types des éléments qui constituent le système.

I.   Connexion en série :

On appelle connexion en série, un système composé de plusieurs éléments telle que la sorite de l’un constitue l’entrée du suivant :

 De ce schéma fonctionnel on a :

D’où

On constate que la fonction de transfert générale représente le produit de toutes les fonctions de transfert en série, d’où :

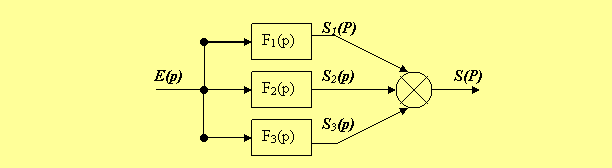
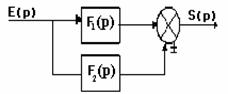
II.  Connexion en parallèle :

On appelle connexion en parallèle, un système composé de plusieurs éléments telle que l’entrée d’un élément constitue l’entrée du système et la somme des sorties de tous les éléments constitue la sortie du système. 

On constate que la fonction de transfert générale est la somme des fonctions de transfert de tous les éléments :

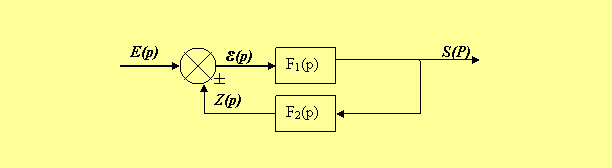
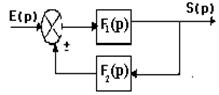
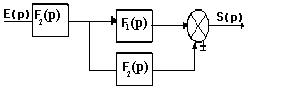
III.    Connexion en opposition parallèle :

Le schéma fonctionnel d’une telle connexion est :

 F_d(p) : Fonction de transfert de la chaîne direct d’action.

F_r(p) : Fonction de transfert de la chaîne de retour ou de réaction.

La fonction de transfert de la boucle fermée est équivalente au rapport suivant :

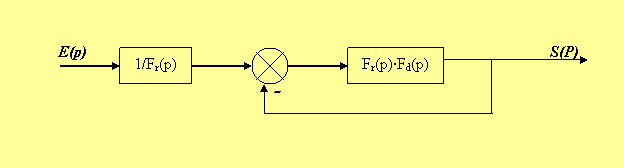
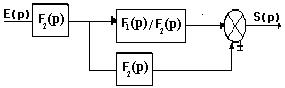
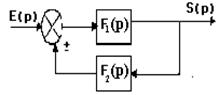
Le signe–indique que la chaîne de retour est positive.

Le signe+ indique que la chaîne de retour est négative.

IV.    Réduction à un système à retour unitaire :

L’étude de tous les asservissements linéaires à une boucle se ramène à celle des asservissements à retour unitaire.

On appelle système à retour unitaire un système ou le signal de retour coïncide avec le signal de sortie : F_r(p)=1

Soit le schéma fonctionnel d’un système à retour non unitaire :

D’où la fonction de transfert en boucle fermée est :

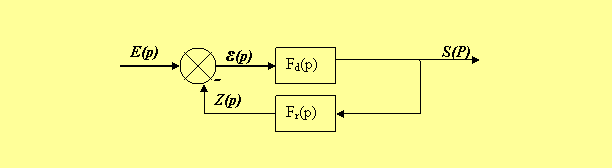
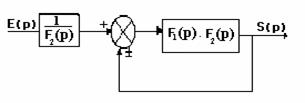
Une transformation du schéma fonctionnel, nous permet de rendre ce système, en un système à retour unitaire :

La fonction de transfert de ce système en boucle fermée :

Il en résulte que les fonctions de transfert des deux schémas sont identiques.

 V.       Tableau des transformations des schémas fonctionnels :

Transformation équation Schéma fonctionnel Schéma fonctionnel équivalant Association d’éléments en cascade. S(p)=F1(p)·F2(p)·E(p) Association d’éléments en parallèle ou en suppression d’une boucle d’action. S(p)=[F1(p)±F2(p)]·E(p) Elimination d’une boucle de retour. S(p)=F1(p)·[E(p)±F2(p)·S(p)] Retrait d’un élément d’une boucle de retour. S(p)=F1(p)·[E(p)±F2(p)·S(p)]

[Home] [Introduction] [Sommaire] [Cours] [Chapitre I] [Chapitre II] [Capitre III] [Chapitre IV] [Chapitre V] [Chapitre VI] [Chapitre VII] [Chapitre VIII] [Exercices]