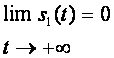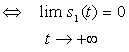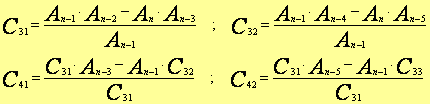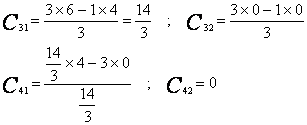|
|
||||||||||||||||||||
|
Download |
||||||||||||||||||||
 |
|
Stabilité des systèmes asservis I. Définition 01: La définition générale de la stabilité d’un système asservis linéaire se ramène simplement aux amplitudes du système de revenir à son état d’équilibre permanent après avoir subi une perturbation. II. Définition 01 :On dit qu’un système est stable si la réponse à une impulsion unité tend vers zéro quand le temps tend vers l’infini. Soit un système décrit par l’équation différentielle suivante :
La solution de cette équation a la forme suivante : s(t)=s1(t) +s2(t) Où : s1(t) : est la réponse permanente (l’équation sans second membre). s2(t) : est la réponse transitoire (l’équation avec second membre). Le système est stable si :
Par conséquent on doit résoudre l’équation suivante :
Cette équation différentielle a l’équation caractéristique suivante :
On sait que la solution s(t) est définie à partir de la solution de l’équation (3). 1ierCas : toutes les racines son réelles : s(t) à la forme suivante :
où : C1, C2,…,Cn : sont des constantes d’intégration. P1, P2,…, Pn : sont les racines de l’équation caractéristique (3). Le système est stable
2ieme Cas : si les racines sont complexes : P1 = α + jβ P2 = α - jβ La solution s(t) a la forme suivante :
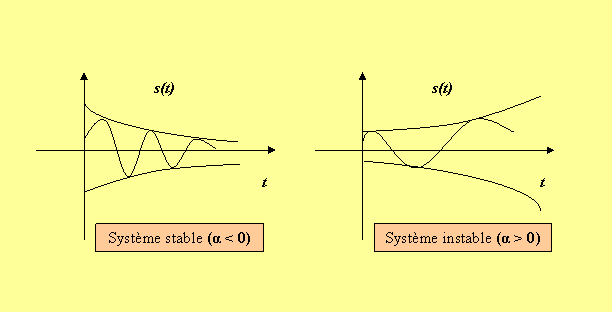
La réponse du système dépend de α(partie réelle).
Donc le système est stable si les parties réelles des racines de l’équation caractéristique sont négatives. 3ieme Cas : si les racines de l’équation caractéristique sont imaginaires pures P=±jω : La solution s(t) est un cosinus ou sinus (système juste oscillant) la limite de la stabilité .
4ieme Cas : si les racines sont nulles P=0 : s(t)=Cte (constante) système astatique .
Conclusion : · Un système est stable si toutes les partie réelles des racines de l’équation caractéristique sont négatives. · Si au moins l’une des racines de l’équation caractéristique a une partie réelle positive le système est instable. III. Critère de ROUTH : La détermination des racines de l’équation caractéristique n’est toujours pas évidente, surtout dans le cas ou l’ordre (n) du système est grand. C’est pour cette raison qu’on utilise le critère de ROUTH pour déterminer la stabilité des systèmes. Soit l’équation caractéristique du système :
On applique la règle de ROUTH, en utilisant une table qu’on appelle table de ROUTH, définie comme suit :
Où :
Pour que l’équation caractéristique ne possède que des racines a parties réelles négatives, il faut et il suffit que tous les termes de la première colonne de la table de ROUTH soient du même signe. Le nombre de changement de signe correspond au nombre de racines à parties réelles positives. Remarque : Il peut arriver que la première colonne du tableau de ROUTH possède un pivot nul ; on peut continuer le tableau en remplaçant ce pivot par ε, nombre réel arbitrairement petit, positif ou négatif. Exemple : 1. Soit l’équation caractéristique : p3+3p2+6p+4=0 La table de ROUTH s’écrit de la manière suivante :
Il n’y a aucun changement de signe dans la première colonne de la table de ROUTH, donc le système est stable. 2. Soit l’équation caractéristique : p3+2p2+3p+8=0 La table de ROUTH s’écrit de la manière suivante :
On remarque qu’il y’a deux changements de signe dans la première colonne (1, 2,-2, 8) de (2)à(-2) et (-2)à(8) ; donc le système a deux racines à parties réelles positives (système instable).
|
|
[Home] [Introduction] [Sommaire] [Cours] [Chapitre I] [Chapitre II] [Capitre III] [Chapitre IV] [Chapitre V] [Chapitre VI] [Chapitre VII] [Chapitre VIII] [Exercices] |