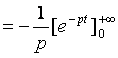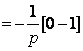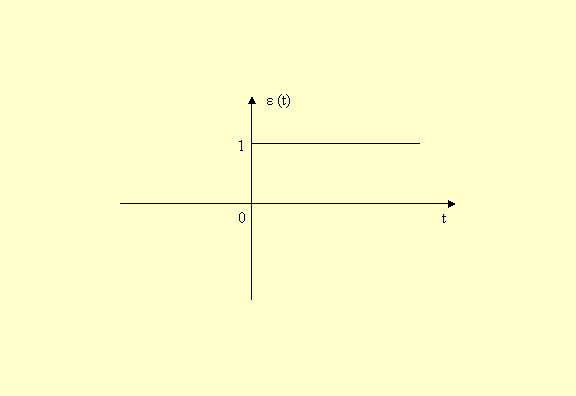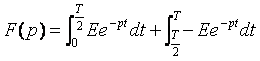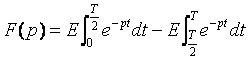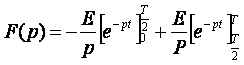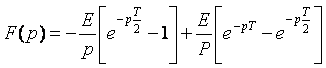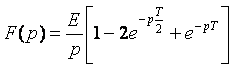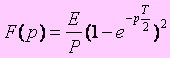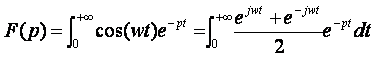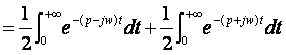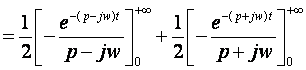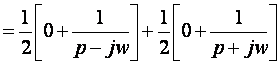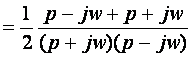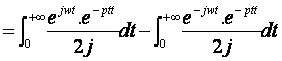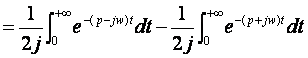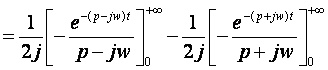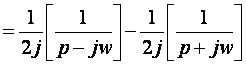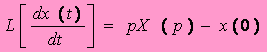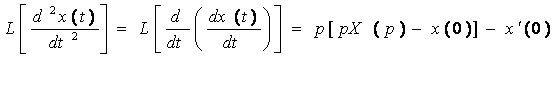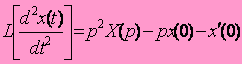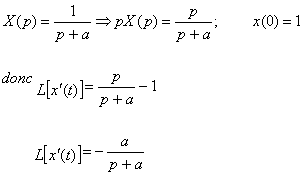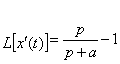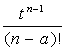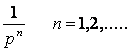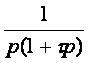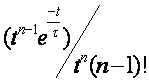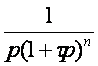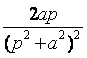|
|
||||||||||||||||||||
|
Download |
||||||||||||||||||||
 |
|
Rappels de mathématique
I. Définition de la transformée de Laplace : On appelle transformée de Laplace de f et notée F, ou encore Lf,la fonction définie sur l’ensemble des nombres complexes p tels que Re (P) > a par la formule :
Propriétés : La linéarité de l’intégrale montre que la transformation de Laplace est linéaire :
II. Applications : 1. Fonction de HEAVISIDE ou échelon unité : La fonction constante et égale à 1 n’admet pas de transformée de Laplace puisqu’elle n’est pas intégrable sur l’intervalle ]-∞, +∞ [ , c’est pourquoi l’on introduit la fonction ε (t) de HEAVISIDE, ou échelon unité, définie par :
Donc :
D’où
2. Cas de fonction périodique : Chercher la transformée de Laplace du signale rectangulaire de période T définie par :
La formule générale s’écrit :
III. Exercices : Calculer les transformées de Laplacede f(t)=cos(wt) et g(t)=sin(wt) sachant que :
On tire :
III.1 : F(p)= ?
D’où :
III.2 :G(p)= ?
D’où :
IV. Propriétés des transformées de Laplace : 1. Théorème de la dérivation :
Pour déterminer la transformée de Laplace de la dérivée de x(t), ou on a :
Finalement :
D’où :
Application: x(t)=
Déterminer
2. Théorème des transformées de Laplace : Soitx(t), L[x(t)]=X(p), Si
Selon le théorème de la dérivation : X(p) = p Y(p) - y(0) D’où :
V. Tableau des transformées de Laplace :
|
|
[Home] [Introduction] [Sommaire] [Cours] [Chapitre I] [Chapitre II] [Capitre III] [Chapitre IV] [Chapitre V] [Chapitre VI] [Chapitre VII] [Chapitre VIII] [Exercices] |
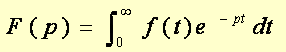 …… (1)
…… (1)