|
|
||||||||||||||||||||
|
Download |
||||||||||||||||||||
 |
|
Méthodes d’analyse des systèmes linéaires a une variable I. Calcul de la réponse d’un système linéaire a une entrée quelconque : 1. Notion de fonction de transfert et de schéma fonctionnel : Pour calculer la réponse s(t)d’un système linéaire a entrée quelconque e(t), on peut applique la transformée de Laplace a l’équation différentielle linéaire a coefficients liant e(t) et s(t), équation que l’on peut mettre sous la forme générale suivante :
On suppose jusqu'à l’application au système linéaire de l’entrée e(t), l’entrée et la sortie du système sont nulles (conditions initiales nulles). Dans ces conditions
On a :
En remplaçant dans (1) e(t), s(t) et leur dérivées successives par leurs transformées de Laplace, il vient la relation suivante :
On désigne par F(p) et on appelle fonction de transfert du système, le rapport des transformées de Laplace de la sortis et de l’entrée du système lorsque les conditions initiales sont nulles :
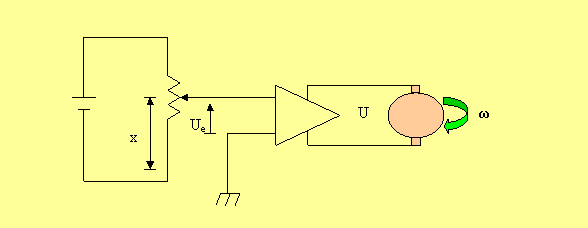
Un système est généralement compose d’éléments ou groupes d’éléments distincts dont chacun d’eux est un système linéaire représentable lui-même par un dipôle et caractérisé par une certaine fonction de transfert ; si la grandeur de sorite de chaque élément ou group d’élément suivant le système, peut être symbolisé par un ensemble de dipôle connectés entre eux qui représentent ce que l’on appel son schéma fonctionnel. Le système de la figure suivante permet de commander avec une énergie réduite la vitesse de rotation ωd’un moteur électrique à courant continu de grande puissance au moyen d’un potentiomètre alimenté en courant continu; moyennant certaines hypothèses, il existe des relation linéaire entre la position x du curseur du potentiomètre et de la tension ue entre le curseur et la masse, entre la tension u de sortie de l’amplification et la tension ue, et entre la vitesse de rotation ω du moteur et la tension u.
Le système considérer peut donc être symbolise par le schéma fonctionnel suivant :
Représenter un système par un dipôle suppose que la sortie de chaque élément dépend uniquement de son entrée et de sa fonction de transfert F(p). Dans ces conditions, la fonction de transfert F(p)d’un système représenté par un schéma fonctionnel de n dipôles, connectés entre eux est égale aux produit des fonction de transfert F1(p), F2(p),…, Fn(p) de chacun des éléments, pour chaque dipôle on a en effet :
E1(p)=F1(p) . E(p) E2(p)=F2(p) . E1(p)
S(p)= Fn(p) . En-1(p)
En multipliant entre eux les premiers et les second membres de ces égalité, il vient :
Avec F(p)=F1(p).F2(p)…Fn(p)
II. Forme générale de la fonction de transfert d’un système linéaire : Une fonction de transfert F(p) se présente d’après (2) sous la forme du quotient de deux polynômes en p. Désignons par Zi les racines du numérateur et par Pj celles du dénominateur de F(p) ; Ziet Pj sont appelés respectivement les zéro et les pôles de F(p) . En général, F(p) se présente sous la forme générale suivante :
Ziet Pj peuvent être nulles, réelles ou imaginaires conjuguées et chacune d’elles peut être d’un ordre quelconque, on peut donc écrire le numérateur et le dénominateur de F(p) sous la forme de produits contenant les termes tels que :
On appellera gain de la fonction de transfertF(p)le facteurk dont l’expression est donnée en(4).
III. Réponse temporelle d’un système linéaire : E(p) désignant la transformée de Laplace de l’entrée e(t) d’un système linéaire de fonction de transfert F(p), la réponse temporelle s(t) du système est :
Si l’on désigne par rj les résidus de la fonction F(p).E(P).eptdp, relatifs aux n pôles p de cette fonction, la fonction, la réponse s(t) est donnée par l’expression générale :
que l’on peut mettre sous la forme :
Si la sortie d’un système linéaire tend vers zéro lorsque son entrée s’annule, ce qui est la définition d’un système stable, la partie
|
|
[Home] [Introduction] [Sommaire] [Cours] [Chapitre I] [Chapitre II] [Capitre III] [Chapitre IV] [Chapitre V] [Chapitre VI] [Chapitre VII] [Chapitre VIII] [Exercices] |
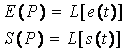
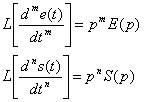
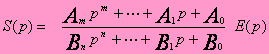
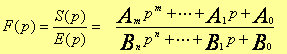 …(2)
…(2)


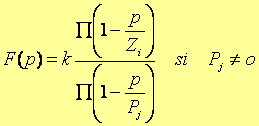 .......(4)
.......(4)
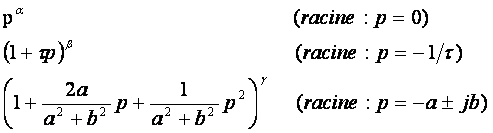

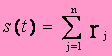

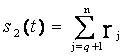 de sa réponse s(t) tend vers zéro quant
de sa réponse s(t) tend vers zéro quant