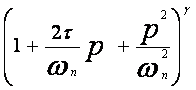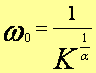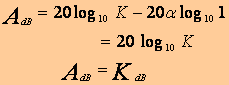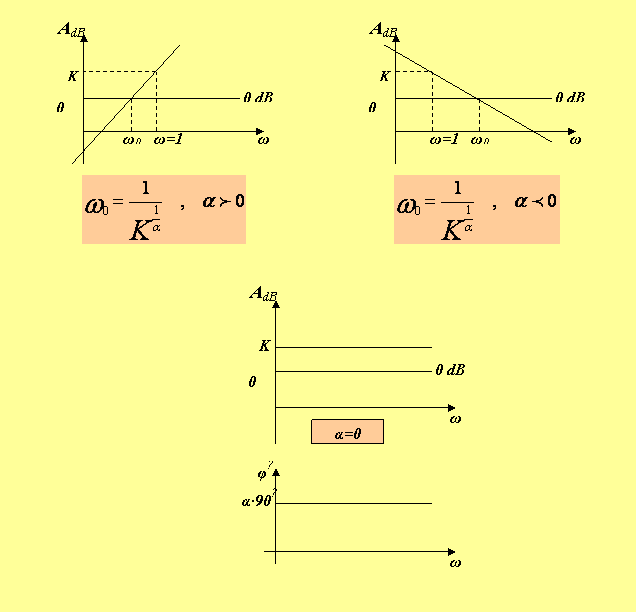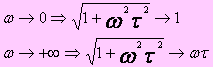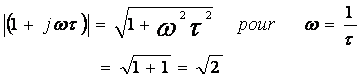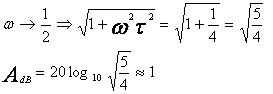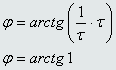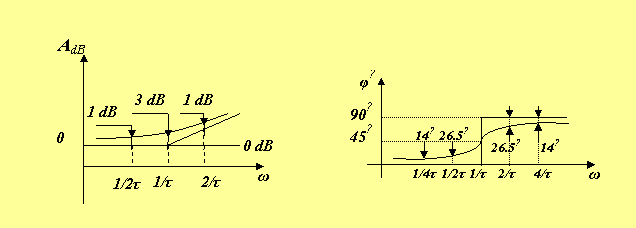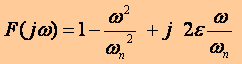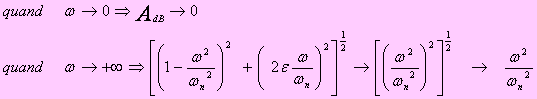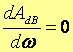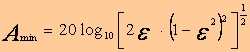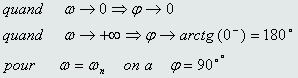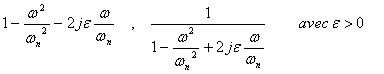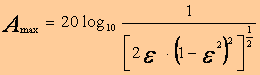 |
|
|
|
|
|
|
||||||||||||||
|
||||||||||||||||||||
 |
||||||||||||||||||||
|
Download |
||||||||||||||||||||
 |
||||||||||||||||||||
 |
|
||||||||||||||||||
|
Diagrammes et Abaques Ce chapitre a pour objet la représentation de la réponse en fréquences T(jω) en boucle ouverte et F(jω) en boucle fermée d’un système asservi linéaire au moyen de diagrammes de différents types. Pratiquement, il est plus intéressant de faire l’étude de la synthèse d’un tel système à partir de T(jω) [le gain K intervient alors linéairement]. En général, on représente donc la réponse en fréquences en boucle ouverte : Les abaques permettent de déterminer graphiquement la réponse en fréquences en boucle fermée F(jω) à partir de T(jω). I. Diagramme de BODE : La représentation dans le plan de BODEd’une réponse en fréquences consiste à tracer séparément, en fonction de la pulsation ω, le module et l’argument de cette réponse, qui représentent respectivement l’affaiblissement et le déphasage subis par des signaux sinusoïdaux de différentes pulsations, appliqués à l’entrée du système qui possède la réponse en fréquence considérée. Une fonction en boucle ouverte se présente, sous l’une des formes du produit de termes de la forme : K p α (1+τp)β
α , β , γ étant des nombres entiers, positifs, négatifs ou nuls. En pratique, on représente en fonction de ω, le module A deT(jω) exprimé en décibels (dB) soit :
L’argument d’un produit de quantités complexes étant égal à la somme des arguments de chacun des termes du produit, la courbe arg[T(jω)], encore appelée diagramme des phases. II. Détermination des diagrammes d’amplitude et de phase des différents termes : II.1. Terme k(jω)α : Le diagramme ‘d’amplitude de ce terme est la courbe A(ω) :
soit :
Cette relation montre que la courbe
Ce papier est limité verticalement, a gauche ou a droite par l’axe de graduation de A et horizontalement, en haut ou en bas par l’axes de graduation des pulsations. Soulignions que le point ω=0 n’apparaît pas sur le diagramme, puisque l’on représenteω sur une échelle logarithmique. De plus, la droite A = 0 dB, appelée axe (0 dB) , est généralement distincte de l’axe des pulsations ω. Pour une octave, c'est-à-dire pour un intervalle(ω , 2 ω), la pente de la droite A(ω) est :
Cette droite coupe l’axe (0 dB) en un point ω0 tel que :
Soit :
Enfin pour ω=1
Si α=0,AdBest une droite horizontale d’ordonnée KdB.
II.2. Terme (1+jωτ)β : Considérons le terme (1+jωτ) (β=1) et τ > 0 correspondant à une racine négative p=-1/τ
Le diagramme d’amplitude du terme considéré possède deux asymptotes : les droites A=1 et A=ωτ. La première asymptote est confondue avec l’axe (0 dB) puisque :
La deuxième asymptote est une droite de pente 6dB/octave qui coupe l’axe (0 dB) à la pulsation (appelée parfois pulsation de cassure) ω= 1/τ (ωτ=1, soit 0dB) Pour cette pulsation, la courbe réelle d’amplitude possède une ordonnée égale à 3dB c'est-à-dire :
Pour les pulsations ω=1/2τ et ω=2/τ, on peut vérifier que ses ordonnées sont supérieures de 1dB à celles de ses asymptotes. En effet :
D’une façon générale, un diagramme réduit à ces asymptotes est appelé digramme asymptotique.
Le diagramme de phase du terme (1+jωτ)est la courbe :
Soit
Quand :
Pour ω=1/τ
Donc
On peut vérifier en TD les poins suivants :
…<… inférieures à celles du diagramme asymptotique. On constate donc, que dans un plan semi logarithmique, la courbe est symétrique par rapport au point (ω=1/τ , φ=90˚). Si l’on considère maintenant le terme à (1-jωτ) avec τ > 0 correspondant à une racine réelle positive p=1/τ du numérateur de T(p), son module est identique à celui de (1+jωτ). Son argument est identique en valeur absolue mais de signe opposé à celui de (1+jωτ).
Des termes de la forme :
ont respectivement des modules, exprimés en décibels et arguments identique en valeurs absolus, mais des signes opposés a ceux de : (1+jωτ)et (1-jωτ). Enfin si β >1, les diagrammes d’amplitude et de phase correspondants sont obtenus par β additions graphiques d’un terme de l’une des formes mentionnées ci-dessus. II.3. Terme 1 - ω2/ωn2 + j2εω/ωn : On a vu que pour les fonctions de transfert de la forme
avec :
d’où :
Le diagramme d’amplitude d’un terme de cette forme est la courbe :
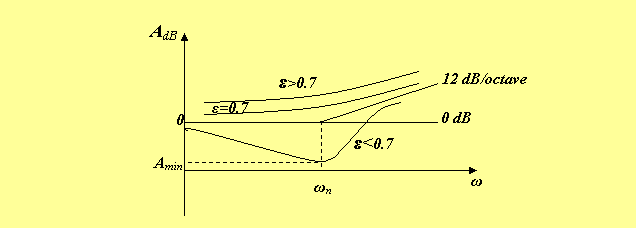
Ce qui met en évidence l’existence d’une seconde asymptote de pente 12 dB/octave, qui coupe l’axe (0 dB) à la pulsation ω=ωn. La courbe réelle dépend du paramètre ε, l’amplitude A passe par un minimum Amin pour une pulsation ωRtel que :
soit pour
donc l’existence et la valeur de ωR dépendent de ε. 1ierCas :
La valeur du minimum de l’amplitudeA est la suivante :
si ε est assez petit on a approximativement
2ieme Cas : Lorsque ε>0.7 on a AdB est toujours supérieur a (0 dB). 3ieme Cas : Pour ε=0.7 le minimum a lieu pour la pulsation ω=0.
Représentation de la phase :
connaissant les variation en fonction deω du module et l’argument d’un terme de la forme précédente, il est facile d’en déduire ceux des terme de la forme :
En pratique on vérifie que ε < 0.7 , le module A passe par un maximumAmax dont l’expression se déduit facilement de l’étude faite plus haut.
ce maximum a lieu pour une pulsation :
|
est une droite ; il est donc commode de tracer A en fonction de
, ce qui revient en pratique à tracer A en fonction de ω, les valeurs de ωportées sur une échelle logarithmiques. A exprimé en dB est porté sur une échelle linéaire et en emploie donc du papier semi logarithmique.
qui possèdent deux racines conjuguées
, qu’il est plus commode d’utiliser la forme suivante :
dans le cas ou 1-2ε2 ≥ 0
|
[Home] [Introduction] [Sommaire] [Cours] [Chapitre I] [Chapitre II] [Capitre III] [Chapitre IV] [Chapitre V] [Chapitre VI] [Chapitre VII] [Chapitre VIII] [Exercices] |