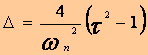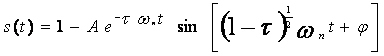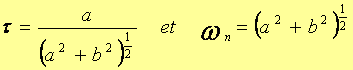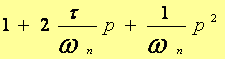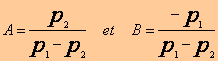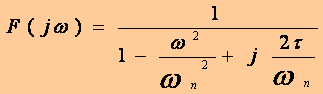Download

Analyse des systèmes linéaires 

On entend par analyse d’un système la recherche expérimentale et l’étude des propriétés de sa fonction de transfert.   

Il s’agit d’analyse transitoire et de l’analyse harmonique.

Dans l’analyse transitoire, on s’intéresse au régime transitoire de la sortie d’un système au quel on applique l’un ou l’autre de certains signaux d’entrée typiques (impulsion,échelon unitaire, …)

Dans l’analyse harmonique, on considère les régimes permanents de sortie correspondant à des entrées variant sinusoïdalement à différentes fréquences.

I.       Analyse transitoire :

1. Réponse d’un système linéaire à  impulsion unitaire :   

Une impulsion unitaire  peut être définie comme la limite quand A tend vers l’infini, d’une impulsion d’amplitude A  et de durée  ce signal est appelé « unitaire » car :

Il a pour transformée de Laplace :

Donc la transformée de Laplace de la réponse à impulsion unitaire d’un système linéaire de fonction de transfert F(p) est :

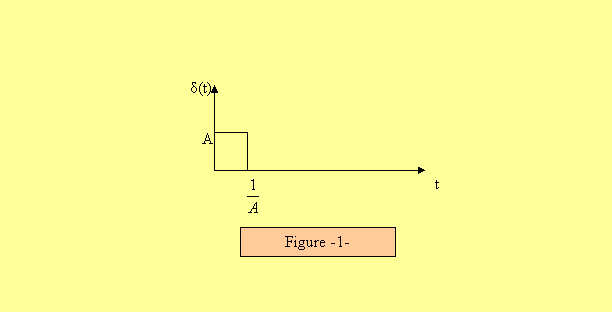
2. Réponse d’un système linéaire à un échelon unitaire :

Un échelon unitaire est définie comme la limite lorsque tend vers zéro du signal représenté sur la figure suivante :

Ce signal a pour dérivée celui de la figure 1

Il en résulte que la réponse d’un système à impulsion unitaire est la dérivée de sa réponse à un échelon unitaire, la transformée de Laplace S(p) de la réponse d’un système linéaire de fonction de transfert F(p) à un échelon unitaire est :

Soit

II.    Analyse harmonique :

On va calculer le régime permanent correspondant à une entrée sinusoïdale :

signal d’amplitude unité et de pulsation ω débitant a l’instant t=0 .

la transformée de Laplace de ce signal a pour expression :

La sortie correspondante d’un système linéaire de fonction de transfert F(p) a pour transformée de Laplace :

Il lui correspond un régime permanent harmonique :

,et étant les résidus de E(p).F(p).e^pt relatifs aux deux pôles de E(p) :

P₁=jω

P₂=-jω

Ces résidus ont pour expressions :

La partie réelle de F(jω), qui ne contaient que  des puissances paires de ωet sa partie imaginaire qui ne contient que des puissances imaginaires de ωsont des fonctions respectivement paire et impaire de ω et les deux nombres complexes F(jω) etF(-jω) sont conjugués.

En les écrivant sous la forme exponentielle :

Il vient par le régime permanent harmonique :

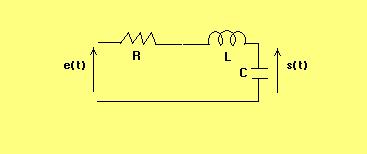
La réponse permanente à un signal sinusoïdale de pulsation ω, appliqué au temps t=0, est donc un signal sinusoïdal de même pulsation ω, dont l’amplitude et la phase sont le module et l’argument de la fonction F(jω) obtenue en remplaçant p par jω dans la fonction de transfert F(p).

Ce résultat montre que la connaissance de la fonction de F(jω), appelée réponse en fréquences du système est équivalant à celle de sa fonction de transfert, c'est-à-dire qu’elle le caractérise complètement.    

 III. Exemples de réponses transitoires et de réponses harmoniques  :

1.système du premier ordre :

 Soit le réseau électrique suivant :

L’équation différentielle régissant ce système s’écrit :

en posant RC = τ

la fonction de transfert de ce système a pour expression :

1.1  Analyse transitoire :

a. Réponse à un échelon unitaire :

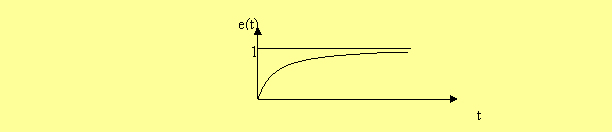
la réponse temporelle correspondante a pour expression :

     elle a une allure représentée sur la figure suivante :

Au bout d’un temps assez long pour que la partie transitoire de la réponse puisse être considérée comme négligeable, le signal de la sortie se trouve pratiquement confondu avec le signal d’entrée , le signal a alors atteint son régime permanent. Le paramètre τ caractérise la durée du régime transitoire de la réponse s(t) ; on l’appelle constante de temps du système.

b.   Réponse à un signal et)= t u(t) :

  D’où

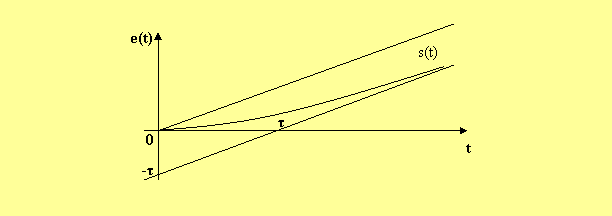
Dont l’allure est la suivante :

   Cette réponse comporte un régime permanent s₁(t)=t-τavec lequel elle se confond lorsque la   partie s₂(t)= τ e^-t/τ devient négligeable.

       Comme dans le cas précédant, la durée de ce régime transitoire est caractérisée par le paramètre τ.

1.  Réponse harmonique :

La réponse en fréquence du système considéré est le nombre imaginaire :

 2.   Système du deuxième ordre:

   L’équation reliant e(t)et s(t) est la suivante :

La fonction de transfert du système s’écrit :

2.1  Analyse transitoire :

Soit :

L’expression de la réponse temporelle correspondante dépend des racines de l’équation :

… (1)

Dans le discriminant Δs’écrit :

Le signe de Δdépend de la valeur par rapport a l’unité de 

On pose    ;     Soit      τ > 0       et      .

L’expression du discriminant devient la suivante :

·       Si τ < 1

L’équation(1) possède deux racines imaginaires conjuguées et la réponse temporelle est :

Avec :                

Et                            

En régime permanent, le signal de sortie et identique au signal d’entrée.

En régime transitoire, la réponse temporelle présente des oscillations est sont allure représentée sur la figure 3 dépend des paramètres τ et .     

Pour donnée, l’exponentielle décroît d’autant plus vite que τ est grand ; pour cette raison, τ est appelé coefficient d’amortissement.

Il est plus commode de faire apparaître τet dans l’expression de tout terme du second ordre figurant dans une fonction de transfert, terme de forme :

Correspondant a deux racines imaginaires conjuguées –a ± j b.

L’introduction des paramètres τet dans l’expression précédente revient à poser :

Un terme du second ordre prend donc finalement la forme :

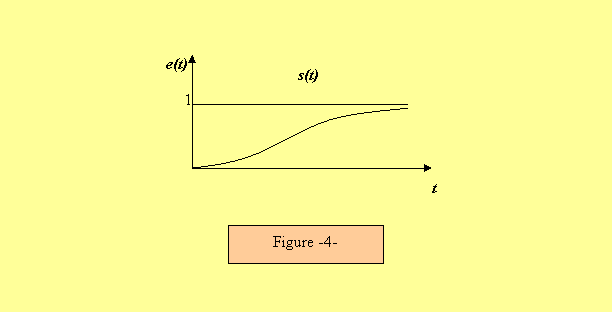
·       Si τ > 1

La réponse du système est apériodique (figure 4)

Si l’on désigne par les racines réelles négatives que possède l’équation (1), la réponse temporelle a pour expression :

Avec :  

·       Si τ = 1

La réponse apériodique est la suivante :

2.2.Réponse harmonique :

La réponse en fréquence du système considéré est le nombre imaginaire obtenu en remplaçant p par jωdans l’expression de sa fonction de transfert :

Qui s’écrit en fonction de τ et

[Home] [Introduction] [Sommaire] [Cours] [Chapitre I] [Chapitre II] [Capitre III] [Chapitre IV] [Chapitre V] [Chapitre VI] [Chapitre VII] [Chapitre VIII] [Exercices]
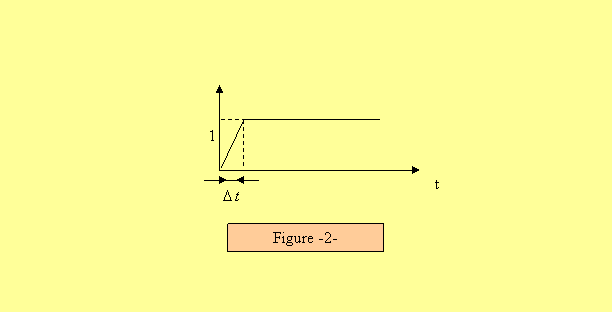
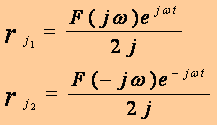
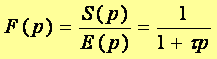
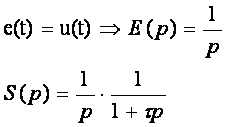
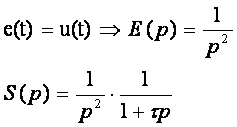
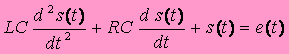
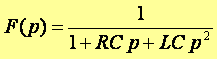
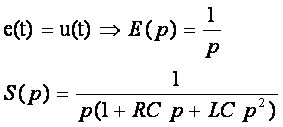
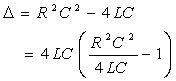